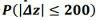Scroll to:
The study of the efficiency of navigation system integration algorithms based on the extended Wiener filter
https://doi.org/10.26467/2079-0619-2025-28-5-22-40
Abstract
Integration of the resulting output signals of the global navigation satellite system (GNSS) and the inertial navigation system (INS) is designed to ensure reliable, safe and stable performance of the aircraft navigation system. To achieve this goal, it is necessary to meet the following requirements for the obtained navigation parameters: high accuracy, continuity of information provision during long-term operation, reliability of the integration algorithm with acceptable computational costs of the aircraft onboard electronics. This paper examines the extended Wiener method for integration of GNSS and INS navigation systems under conditions of an unstable navigation data supply. Processing of navigation information from measuring devices is the basis for ensuring flight safety and aircraft control accuracy. Navigation parameters are measured as part of an integrated modular avionics system, including global navigation satellite systems (SRNS), inertial navigation system (INS), GPS/GLONASS and radar systems. The results of modeling the error in aircraft speed and position after applying the extended Wiener filter are presented. The effectiveness of the proposed algorithm was assessed based on strict statistical criteria.
Keywords
For citations:
Zasukhin A.S., Budaev V.D., Sizikov D.O. The study of the efficiency of navigation system integration algorithms based on the extended Wiener filter. Civil Aviation High Technologies. 2025;28(5):22-40. https://doi.org/10.26467/2079-0619-2025-28-5-22-40
1. Introduction
The navigation system is the main source of parametric information for providing the crew and aircraft navigation systems with data on the aircraft attitude and its motion characteristics. The main sources of navigation information are the satellite navigation system (SNS) and the inertial system (INS) [1][2]. However, each individual navigation system does not fully satisfy the requirements of accuracy, noise immunity, autonomy and fault tolerance.
The disadvantage of the inertial navigation system is the accumulated error (drift) during long-term operation, which grows proportionally to the operating time or even faster depending on the accuracy class of the system. The disadvantage of the global navigation satellite system is its dependence on external interference, signal interruption and other factors that can prevent accurate coordinate calculation.
The integration of the signals from the two navigation systems listed above makes it possible to compensate for the disadvantages of each individual system and use their advantages in operation. In particular, highly accurate but drift-prone inertial navigation system data can be corrected by relatively stable, but less accurate and interference-prone global navigation satellite system data. Algorithms for the integration of two or more sources of navigation information allow for the provision of aircraft systems with correct navigation parameters that have been optimally filtered.
This paper discusses an improved algorithm for integrating navigation systems based on the extended Wiener filter, which provides statistically optimal processing of data from various sources, taking into account their stochastic characteristics [3][4].
2. Mathematical justification for the choice of an extended Wiener filter for integrating navigation systems
2.1. Comparative analysis of the methods for integrating navigation systems
Various methods are currently used to solve the problem of integrating navigation data, including the Kalman filter, the Wiener filter, fuzzy logic methods and neural network approaches. The choice of the optimal method is determined by the specific application conditions, accuracy requirements and computing resources of the onboard equipment.
The Kalman filter is one of the most common methods of integration and has a number of advantages: recursive structure; the ability to work in real time; taking into account the dynamics of the system [5]. However, for the Kalman filter to work effectively, precise knowledge of the system dynamics model and noise characteristics is required, which is not always available in real aircraft operating conditions.
The extended Wiener filter, unlike the Kalman filter, does not require full knowledge of the system dynamics model and can operate effectively using only statistical characteristics of signals and noise. This makes it more stable under conditions of model uncertainty and in the presence of non-stationary interference [1][6]. Below we present a mathematical justification for choosing the extended Wiener filter to solve the problem.
2.2. Theoretical foundations of the extended Wiener filter
The classical Wiener filtering problem is formulated as the problem of minimizing the mean square error between the true signal 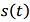 and the estimate of this signal
and the estimate of this signal 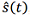 , obtained by linear filtering of a noisy observation
, obtained by linear filtering of a noisy observation 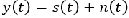 , where
, where 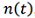 is the additive noise.
is the additive noise.
For the discrete case applicable to navigation systems, the extended Wiener filter can be represented as
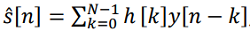 (1)
(1)
where 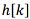 is the impulse response of the filter, Ν is the filter order.
is the impulse response of the filter, Ν is the filter order.
Unlike the classical Wiener filter, the extended filter takes into account the non-stationarity of the statistical characteristics of signals and noise, as well as the possibility of integrating more than two data sources. The optimal impulse response of the filter is found from the condition of minimizing the functional:
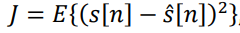 (2)
(2)
where 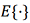 is the mathematical expectation.
is the mathematical expectation.
The solution to this optimization problem leads to a system of Wiener-Hopf equations:
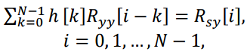 (3)
(3)
where 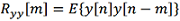 is the autocorrelation function of the observation,
is the autocorrelation function of the observation, 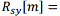
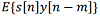 is the mutual correlation function between the true signal and the observation.
is the mutual correlation function between the true signal and the observation.
For the case of integrating several navigation systems, the extended Wiener filter can be represented in vector form:
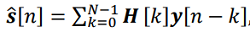 (4)
(4)
where 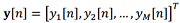 is the vector of observations Μ from different navigation systems,
is the vector of observations Μ from different navigation systems,  is the matrix of impulse responses of the filter.
is the matrix of impulse responses of the filter.
The optimal matrix 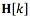 is found from the solution of the Wiener-Hopf matrix equation:
is found from the solution of the Wiener-Hopf matrix equation:
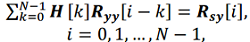 (5)
(5)
where 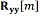 is the autocorrelation matrix of the observations,
is the autocorrelation matrix of the observations, 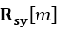 is the mutual correlation matrix between the true signal and the observations.
is the mutual correlation matrix between the true signal and the observations.
2.3. Adaptive modification of the extended Wiener filter
To improve the efficiency of integration of navigation systems under conditions of changing characteristics of signals and interference, an adaptive modification of the extended Wiener filter is proposed. The main idea is to use a sliding window to estimate the correlation functions:
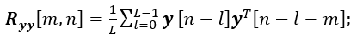 (6)
(6)
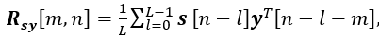 (7)
(7)
where L is the size of the sliding window.
The adaptability of the filter is ensured by periodic recalculation of the matrix of impulse responses based on updated estimates of the correlation functions. The update frequency is determined by the dynamics of changes in the characteristics of signals and interference.
For the case when the true signal 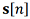 is unavailable (which corresponds to the real situation), a blind identification method is used based on minimizing the mutual information between the components of the estimated signal. This allows us to identify the most informative components of the signal without a priori knowledge of its characteristics.
is unavailable (which corresponds to the real situation), a blind identification method is used based on minimizing the mutual information between the components of the estimated signal. This allows us to identify the most informative components of the signal without a priori knowledge of its characteristics.
3. Methods for assessing the effectiveness of navigation parameter integration algorithms
3.1. Navigation systems used and their characteristics
To evaluate the efficiency of navigation parameter integration algorithms, we will determine the characteristics of the systems operating on board the aircraft. According to research data [1][6], the mean-square errors (MSE) of determining the aircraft location for various navigation systems are:
Inertial Navigation System (INS): σ_"INS" = = 6500 m;
Air Data Computer (ADC): σ_"ADC" = = 11000 m;
Doppler Velocity Sensor (DVS): σ_"DVS" = = 4000 m;
Short Range Navigation System (SHORAN): σ_"SHORAN" = 400 m;
Global Navigation Satellite System (GNSS): σ_"GNSS" = 175 m.
The specified accuracy characteristics are based on experimental data and the results of studies of errors in navigation systems operated on modern civil aviation aircraft [7][8], except for DVS, which is an experimental tolerance, i.e. we assume that there is a DVS with a given standard deviation for experimental testing.
3.2. Research methodology and performance criteria
The study used a mathematical model of aircraft motion as a rigid body with six degrees of freedom. When modeling a flight along a route (fig. 1), a control method using a running point was used [2][9].
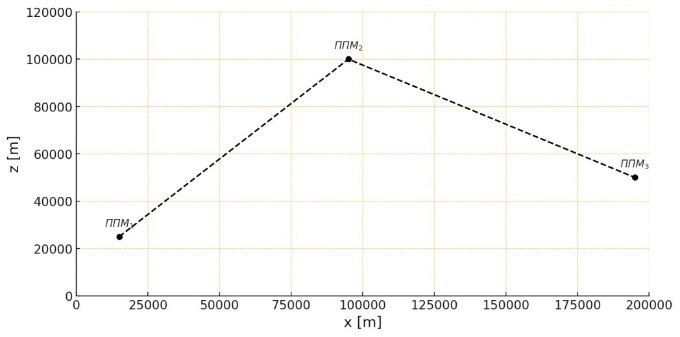
Fig. 1. Route control method of the aircraft
The following indicators are defined for the efficiency criterion:
1) cumulative deviation (ι), describing the deviation of the aircraft position at each moment in time 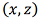 using navigation signals from its position during an ideal flight.
using navigation signals from its position during an ideal flight. 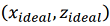 .
.
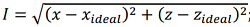 (8)
(8)
2) average lateral deviation 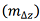 , which reflects the deviation of the flight route from the course line (required track) and is determined by the expression
, which reflects the deviation of the flight route from the course line (required track) and is determined by the expression
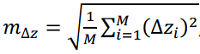 (9)
(9)
where 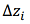 is the deviation from the course line (required track) at the moment of observation i ; M is the number of observations;
is the deviation from the course line (required track) at the moment of observation i ; M is the number of observations;
3) the accuracy of the aircraft reaching the final point of the route 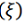 , which is determined by the formula
, which is determined by the formula
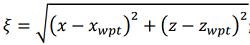 (10)
(10)
4) the probability of keeping the aircraft within the allotted corridor relative to the required track 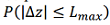 . Considering that the lateral deviation of the aircraft from the required track is a function of many random parameters, the probability density of the parameter can be assumed to be subject to the Gaussian law [10][11–13].
. Considering that the lateral deviation of the aircraft from the required track is a function of many random parameters, the probability density of the parameter can be assumed to be subject to the Gaussian law [10][11–13].
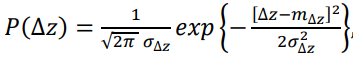 (11)
(11)
where 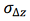 is the variance of the lateral deviation
is the variance of the lateral deviation 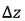 .
.
We will assume that the permissible deviation from the course line does not outweigh 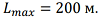 . Therefore, the probability that the aircraft will not go beyond the permissible limit is determined by the expression
. Therefore, the probability that the aircraft will not go beyond the permissible limit is determined by the expression
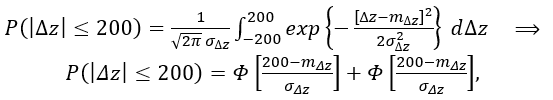 (12)
(12)
where Ф(a) is the tabulated probability integral.
4. Implementation of the integration algorithm based on the extended Wiener filter
4.1. Structural diagram of the integration algorithm
Figure 2 shows the block diagram of the proposed algorithm for integrating navigation systems based on the extended Wiener filter.

Fig. 2. A block diagram of signal integration using an extended Wiener filter
It should be noted that this paper examines the characteristics of modern DVS of a new generation, which have significantly improved technical characteristics compared to previous models. Modern DVS, developed by Luch Design Bureau and other manufacturers, are multifunctional single housing units with digital data output, which significantly simplifies their integration with onboard navigation systems. They are distinguished by high accuracy of speed measurement (error no more than ±0.25%) and drift angle (error no more than ±16 arc minutes) due to the use of frequency modulation and modern algorithms for digital signal processing. Some DVS models, such as the DISS-32-28 and D001, have a wide range of measured speeds (from 180 to 4000 km/h) and operating altitudes (from 1.6 to 30,000 m), making them applicable to both traditional aircraft and advanced unmanned aerial vehicles.
4.2. Mathematical implementation of the extended Wiener filter for navigation systems
With regard to the problem of integration of navigation systems, the extended Wiener filter is implemented as follows. Let there be M navigation systems, each of which provides an estimate of the aircraft state vector:
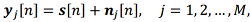 (13)
(13)
where 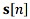 is the true aircraft state vector,
is the true aircraft state vector, 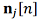 is the error vector of the jth navigation system.
is the error vector of the jth navigation system.
The integration problem supposes finding the optimal estimate 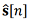 the true aircraft state vector based on observations from all M systems:
the true aircraft state vector based on observations from all M systems:
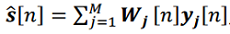 (14)
(14)
where 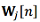 is the matrix of weighting coefficients for the jth navigation system.
is the matrix of weighting coefficients for the jth navigation system.
The optimal weighting coefficients are found from the condition of minimum mean square error:
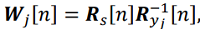 (15)
(15)
where 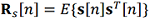 is the covariance matrix of the true state vector,
is the covariance matrix of the true state vector, 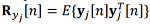
is the covariance matrix of observations of the jth system.
The covariance matrix of the true state vector can be estimated based on a priori data on the aircraft dynamics or using high-precision reference measurements at the stage of system calibration.
Taking into account the non-stationarity of the characteristics of navigation systems, the covariance matrices are estimated recursively:
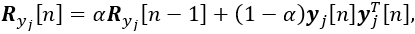 (16)
(16)
where a is the forgetting coefficient, which determines the speed of filter adaptation to changing conditions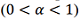 .
.
To initialize the recursive algorithm (16) the initial covariance matrix Ryj[0] can be specified based on the passport characteristics of the errors of the navigation systems or the results of preliminary calibration.
In the event of failure or temporary unavailability of one of the navigation systems, the corresponding weighting coefficients are automatically adjusted taking into account the current estimates of the statistical characteristics of the remaining systems [14–16].
5. Results of the study of the integration algorithm efficiency
5.1. Analysis of the navigation systems accuracy
Figure 3 presents the results of modeling the impact of errors in various navigation systems on the accuracy of maintaining the course line. The shown results represent the absolute deviations of the flight path from the course line (required track) |Δz| at each observation moment.

Fig. 3. Absolute deviation of the flight route from the course line using navigation systems
The analysis of the results shows that the accuracy of maintaining an aircraft on a flight path depends significantly on the mean-square error of the navigation system used. As shown in the graphs, the smallest deviation from the course line is achieved using the Global navigation satellite system, which has the smallest coordinate determination error, while the largest deviation is achieved using the Air Data Computer.
Table 1 shows the results of calculating the mean-square lateral deviation m_Δz for various navigation systems.
Table 1
Determination results
|
Navigation System |
INS |
ADC |
DVS |
SHORAN |
GNSS |
|
Average Lateral Error (), m |
861.4379 |
2188.583 |
416.3014 |
33.9721 |
18.0735 |
|
Lateral Error Variance (), m² |
742076.64 |
4789818.62 |
173286.87 |
1154.11 |
326.65 |
The results confirm that the GNSS with the lowest mean square error provides the best accuracy of maintaining the course line, and the ADC with the highest error provides the worst accuracy.
5.2. The efficiency of integrating using the extended Wiener filter

Figure 4 shows the results of modeling the absolute deviation from the course line when integrating navigation signals using the extended Wiener filter.
Fig. 4. Absolute deviation from the course line when integrating navigation signals using a Wiener filter
The comparison with the results of individual navigation systems (fig. 3) shows that integration provides a significant improvement in the accuracy of maintaining the course line (required track). Moreover, the accuracy of the integrated system exceeds that of the most accurate individual system (GNSS).
Figure 5 shows a comparison of the accumulated deviation I using individual navigation systems and the integration method.

Fig. 5. The dependence of the accumulated deviation I on the results of the integration of navigation systems during flight: a – in a straight line, б – along the route
The graphs clearly demonstrate that signal integration using the extended Wiener filter allows for a significant reduction in cumulative deviation compared to using individual navigation systems.
5.3. Algorithm stability to navigation systems failures
To assess the stability of the proposed algorithm to individual navigation systems failures, situations with an absence of signal from one of the systems were simulated. Figure 6 shows the absolute deviations of the flight path from the course line |Δz| in the absence of a signal as a result of, for example, a malfunction of one of the navigation systems.

Fig. 6. Absolute deviations of the flight path from the course line (required track)
The results show that the proposed integration algorithm remains operational even if one of the systems fails. The accuracy of determining the aircraft position decreases only slightly and remains higher than when using the most accurate system alone. Figure 7 shows the effect of integrating various combinations of four navigation systems on the accumulated deviation I. The characteristic jumps in the graphs (fig. 7) correspond to the moments of an abrupt change in the flight path upon entering a turn (t ≈ 120 s) and the beginning of the stabilization section after completing the turn (t ≈ 240 s). At these moments, the adaptive Wiener filter algorithm rearranges the weighting coefficients in accordance with the change in flight dynamics, which temporarily increases the position estimation error. The simulation results for various combinations of three (figs. 8–10) and two (figs. 11–13) navigation systems confirm the efficiency of the proposed integration algorithm even with a limited set of available systems. For various combinations of combining two navigation systems, the results of determining the absolute deviation |∆z| and the accumulated deviation I are shown in Figures 11–13. From the figures it is clear that the use of the Wiener filter for integrating various systems also improves the accuracy of route maintenance.

Fig. 7. The influence of integrating various four systems on I during flight:
a – in a straight line, b – along a route

Fig. 8. The results of determining the absolute deviation of the flight path
from the course line (required track) during integration of 3 system

Fig. 9. I when flying: a – in a straight line, b – along the route

Fig. 10. Accumulated deviation I when flying: a – in a straight line, b – along the route

Fig. 11. The results of determining the absolute deviation of the flight path from the course line
when integrating two systems

Fig. 12. Accumulated deviation I when integrating two systems: a – in a straight line, b – along the route

Fig. 13. Accumulated deviation I when integrating two systems: a – in a straight line, b – along the route
5.4. Probabilistic characteristics of keeping aircraft within an acceptable airway range
Based on the obtained statistical characteristics of the lateral deviation of the aircraft from the course line, the probabilities of keeping the aircraft within the acceptable airway range of 200 m width were calculated. The results are presented in Table 2.
Table 2
The probability of keeping the aircraft within the acceptable range (200 m)
|
Navigation system/intergration |
Mean-square deviation |
The probability |
|
INS |
862.14 |
0.2321 |
|
ADC |
2188.58 |
0.0914 |
|
DVS |
416.30 |
0.4812 |
|
SHORAN |
33.97 |
0.9999 |
|
GNSS |
18.07 |
0.9999 |
|
Integration of all systems |
12.35 |
0.9999994 |
|
Integration (INS, DVS, SHORAN, GNSS) |
14.21 |
0.9999990 |
|
Integration (DVS, SHORAN, GNSS) |
15.83 |
0.9999987 |
|
Integration (SHORAN, GNSS) |
16.94 |
0.9999983 |
Analysis of the table data shows that integrating navigation systems using the extended Wiener filter significantly increases the probability of keeping an aircraft within the acceptable range compared to using individual navigation systems. Moreover, the highest probability is achieved by integrating all available systems.
6. Mathematical analysis of the reasons for increasing accuracy during integration
To theoretically substantiate the experimental results obtained, we will conduct a mathematical analysis of the effect of integration on the accuracy of aircraft location determination [17].
Let us assume that there are M independent navigation systems, each of which provides an estimate of the aircraft state vector with an error variance. 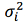 . When data integration is performed using an extended Wiener filter, the resulting error variance is determined by the expression:
. When data integration is performed using an extended Wiener filter, the resulting error variance is determined by the expression:
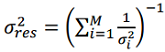 (17)
(17)
For the case of integrating two systems with variances 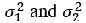 we obtain:
we obtain:
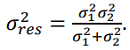 (18)
(18)
Obviously  , that confirms the theoretically observed effect of increasing accuracy during integration.
, that confirms the theoretically observed effect of increasing accuracy during integration.
For an adaptive extended Wiener filter with recurrent estimation of the statistical characteristics of signals and noise, the variance of the resulting error is determined by a more complex expression:
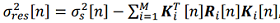 (19)
(19)
where 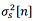 is a priori variance of the state vector,
is a priori variance of the state vector, 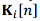 is the gain coefficient of the filter for the ith system,
is the gain coefficient of the filter for the ith system, 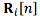 is the covariance matrix of the measurements of the ith system.
is the covariance matrix of the measurements of the ith system.
This expression explains the dependence of the accuracy of the integrated system on the statistical characteristics of individual navigation systems and their mutual correlation effect.
7. Conclusion
A study of the effectiveness of navigation system integration algorithms based on the extended Wiener filter allows us to draw the following conclusions:
1. Integration of navigation system signals using the extended Wiener filter significantly improves aircraft positioning accuracy compared to using individual navigation systems. Moreover, the mean-square lateral deviation from the course line decreases from 18.07 m (for the most accurate GNSS system) to 12.35 m when integrating all available systems.
2. The proposed integration algorithm is highly resilient to failures of individual navigation systems. Even if the most accurate system (GNSS) fails, the aircraft positioning accuracy remains sufficiently high due to the adaptive redistribution of weighting factors in the filter.
3. The probability of keeping an aircraft within an acceptable 200-meter-wide airway range using the integrated system is 0.9999994, which exceeds the corresponding figure for the most accurate standalone system (0.9999 for GNSS).
4. Mathematical analysis confirms that the improved accuracy during integration is a consequence of optimal statistical processing of data from various navigation systems, taking into account their stochastic characteristics.
5. The adaptability of the extended Wiener filter ensures effective integration of navigation systems under changing signal and interference characteristics, which is particularly important for ensuring flight safety in challenging conditions.
Thus, using the extended Wiener filter for integration of navigation systems is an effective method for improving the accuracy, reliability, and safety of aircraft navigation.
References
1. Petrash, V.Ya. (2007). Methods and models of computer-aided aircraft design: Tutorial. Moscow: MAI, 92 p. (in Russian)
2. Blomenhofer, H. (1996). Accuracy, Integrity and availability of GLS-based autopilot coupled aircraft landings. NAVIGATION: Journal of the Institute of Navigation, vol. 43, issue 4, pp. 420–436. DOI: 10.1002/j.2161-4296. 1996.tb01930.x
3. Vindeker, A.V., Parafes', S.G. (2018). Choice of structural material and external gas rudder geometry of declination system of unmanned aerial vehicle. Civil Aviation High Technologies, vol. 21, no. 1, pp. 67–76. DOI: 10.26467/2079-0619-2018-21-1-67-76 (in Russian)
4. Markelov, V.V., Kostishin, M.O., Zharinov, I.O., Nechaev, V.A. (2016). Forming route trajectories for aiborne multi-function displays. Information and control systems, no. 1 (80), pp. 40–49. DOI: 10.15217/issn1684-8853.2016.1.40 (in Russian)
5. Petrash, V.Ya. (2009). Features of automated design of unmanned aerial vehicles with aerogasdynamic control. Moscow: MAI-PRINT, 95 p. (in Russian)
6. Petrash, V.Ya. (2020). Ballistic and mass-geometric design of unmanned aerial vehicles in an educational CAD system: Tutorial. Moscow: MAI, 98 p. (in Russian)
7. Yakovlev, G.A., Masaltseva, E.K. (2018). Modeling the flight course of vertical launching rockets. Tekhnika XXI veka glazami molodykh uchenykh i spetsialistov, no. 17, pp. 393–402. (in Russian)
8. Chen, Q. (1995). Comparison of different k-ε models for indoor air flow computations. Numerical Heat Transfer, vol. 28, no. 3, pp. 353–369. DOI: 10.1080/10407799508928838
9. Du, W., Zhou, H., Chen, W. (2016). Trajectory optimization for agile-turn of vertically launched missile. In: 2016 IEEE International Conference on Mechatronics and Automation, pp. 2110–2115. DOI: 10.1109/ICMA.2016.75 58892
10. Markelov, V.V., Kostishin, М.О., Shukalov, A.V. (2015). Aircraft inertial navigation system pre-takeoff course correction by information from a satellite navigation system. Information and control systems, no. 6 (79), pp. 34–39. DOI: 10.15217/issn1684-8853.2015. 6.34 (in Russian)
11. Ma, H.Y., Cheng, P.F., Huang, H.D. (2016). Research on the complete integrated GPS/INS navigation system of velocity and attitude. Bulletin of Surveying and Mapping, no. 3, pp. 10–14.
12. Murty, C., Chakraborty, D. (2015). Numerical characterisation of jet-vane based thrust vector control systems. Defence Science Journal, vol. 65, no. 4, pp. 261–264. DOI: 10.14429/dsj.65.7960
13. Murty, C., Rao, M.S., Chakraborty, D. (2010). Numerical simulation of nozzle flow field with jet-vane based thrust vector control. Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering, vol. 224, no. 5, pp. 541–548. DOI: 10.1243/09544100JAERO677 (accessed: 15.08.2024).
14. Tan, X., Jian, W, Han, H. (2014). SVR aided adaptive robust filtering algorithm for GPS/INS integrated navigation. Acta Geo-daetica et Cartographica Sinica, vol. 43, no. 6, pp. 590–606. DOI: 10.13485/j.cnki.11-2089. 2014.0093
15. Tekin, R., Atesoglu, O., Leblebici-oglu, K. (2013). Flight control algorithms for a vertical launch air defense missile. In: Advances in Aerospace Guidance, Navigation and Control, in Chu Q., Mulder B., Choukroun D., van Kampen E.J., de Visser C., Looye G. (eds). Springer, Berlin, Heidelberg, pp. 73–84. DOI: 10.1007/ 978-3-642-38253-6_6
16. Yogesh, M., Hari Rao, A.N. (2016). Solid particle erosion response of fiber and particulate filled polymer based hybrid composites: a review. Journal of Engineering Research and Applications, vol. 6, issue 1, pp. 25–39.
17. Jiang, C., Zhang, S.B., Zhang, Q.Z. (2017). Adaptive estimation of multiple fading factors for GPS/INS integrated navigation systems. Sensors, vol. 17, issue 6, ID: 1254. DOI: 10.3390/s17061254 (accessed: 15.08.2024).
About the Authors
A. S. ZasukhinRussian Federation
Alexander S. Zasukhin, The Head of the Training and Simulator Center, Senior Lecturer, the Chair of Aircraft Engine Engineering
Moscow
V. D. Budaev
Russian Federation
Vladislav D. Budaev, Senior Lecturer, the Chair of Aircraft Engine Engineering
Moscow
D. O. Sizikov
Russian Federation
Daniil O. Sizikov, Senior Lecturer, Electrical Systems and Flight Navigation Complexes Maintenance Chair
Moscow
Review
For citations:
Zasukhin A.S., Budaev V.D., Sizikov D.O. The study of the efficiency of navigation system integration algorithms based on the extended Wiener filter. Civil Aviation High Technologies. 2025;28(5):22-40. https://doi.org/10.26467/2079-0619-2025-28-5-22-40



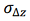 , m
, m