Перейти к:
Исследование эффективности алгоритмов комплексирования навигационных систем на основе расширенного фильтра Винера
https://doi.org/10.26467/2079-0619-2025-28-5-22-40
Аннотация
Комплексирование результирующих выходных сигналов глобальной навигационной спутниковой системы (ГНСС) и инерциальной навигационной системы (ИНС) призвано обеспечить надежную, безопасную и устойчивую работоспособность навигационной системы воздушного судна (ВС). Для достижения этой цели необходимо обеспечить следующие требования к получаемым навигационным параметрам: высокая точность, непрерывность предоставления информации при длительной работе, надежность алгоритма комплексирования при приемлемых вычислительных затратах бортовой электроники ВС. В данной работе исследуется расширенный метод Винера для комплексирования навигационных систем ГНСС и ИНС в условиях нестабильной подачи навигационных данных. Обработка навигационной информации от измерительных устройств является основой обеспечения безопасности полетов и точности управления воздушным судном. Измерение навигационных параметров осуществляется в составе интегральной модульной авионики, включающей спутниковые радионавигационные системы (СРНС), инерциальную навигационную систему (ИНС), GPS/ГЛОНАСС и радиолокационные системы. Представлены результаты моделирования погрешности по скорости и положению ВС после применения расширенного фильтра Винера. Проведена оценка эффективности предложенного алгоритма на основе строгих статистических критериев.
Ключевые слова
Для цитирования:
Засухин А.С., Будаев В.Д., Сизиков Д.О. Исследование эффективности алгоритмов комплексирования навигационных систем на основе расширенного фильтра Винера. Научный вестник МГТУ ГА. 2025;28(5):22-40. https://doi.org/10.26467/2079-0619-2025-28-5-22-40
For citation:
Zasukhin A.S., Budaev V.D., Sizikov D.O. The study of the efficiency of navigation system integration algorithms based on the extended Wiener filter. Civil Aviation High Technologies. 2025;28(5):22-40. https://doi.org/10.26467/2079-0619-2025-28-5-22-40
1. Введение
2. Математическое обоснование выбора расширенного фильтра Винера для комплексирования навигационных систем
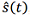 , полученной путем линейной фильтрации зашумленного наблюдения y(t)=s(t)+n(t), где n(t) – аддитивный шум.
, полученной путем линейной фильтрации зашумленного наблюдения y(t)=s(t)+n(t), где n(t) – аддитивный шум. ,(1)
,(1) 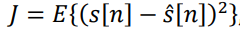 ,(2)
,(2)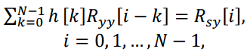 ,(3)
,(3) 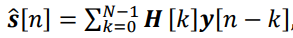 ,(4)
,(4) 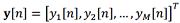 – вектор наблюдений от M различных навигационных систем, H[k] – матрица импульсных характеристик фильтра.
– вектор наблюдений от M различных навигационных систем, H[k] – матрица импульсных характеристик фильтра.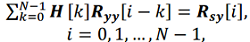
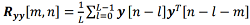 ; (6)
; (6)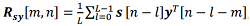 , (7)
, (7) 3. Методы оценки эффективности алгоритмов комплексирования навигационных параметров
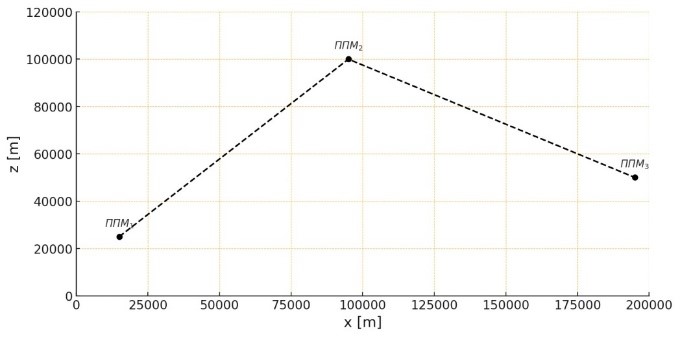
Рис. 1. Маршрутный метод управления ВС
Fig. 1. Route control method of the aircraft
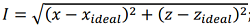 ; (8)
; (8)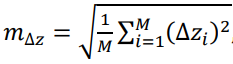 ,(9)
,(9)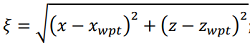 ;(10)
;(10)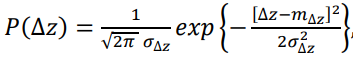 ,(11)
,(11) 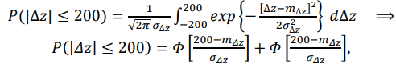 ,(12)
,(12) 4. Реализация алгоритма комплексирования на основе расширенного фильтра Винера

Рис. 2. Структурная схема комплексирования сигналов с помощью расширенного фильтра Винера
Fig. 2. A block diagram of signal integration using an extended Wiener filter
 ,(13)
,(13)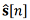 истинного вектора состояния ВС на основе наблюдений от всех M систем:
истинного вектора состояния ВС на основе наблюдений от всех M систем: ,(14)
,(14)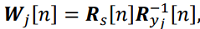 ,(15)
,(15)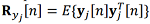 – ковариационная матрица наблюдений j-й системы.
– ковариационная матрица наблюдений j-й системы.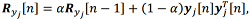 , (16)
, (16)5. Результаты исследования эффективности алгоритма комплексирования

Рис. 3. Абсолютное отклонение маршрута полета от ЛЗП с использованием навигационных систем
Fig. 3. Absolute deviation of the flight route from the course line using navigation systems
Таблица 1
Table 1
Результаты расчета среднеквадратического бокового отклонения
Determination results
|
Навигационная система |
ИНС |
СВС |
ДИСС |
РСБН |
СРНС |
|
Среднее боковое отклонение (), м |
861,4379 |
2 188,583 |
416,3014 |
33,9721 |
18,0735 |
|
Дисперсия бокового отклонения (), м² |
742 076,64 |
4 789 818,62 |
173 286,87 |
1 154,11 |
326,65 |

Рис. 4. Абсолютное отклонение от линии заданного пути при комплексировании навигационных
сигналов с помощью фильтра Винера
Fig. 4. Absolute deviation from the course line when integrating navigation signals using a Wiener filter
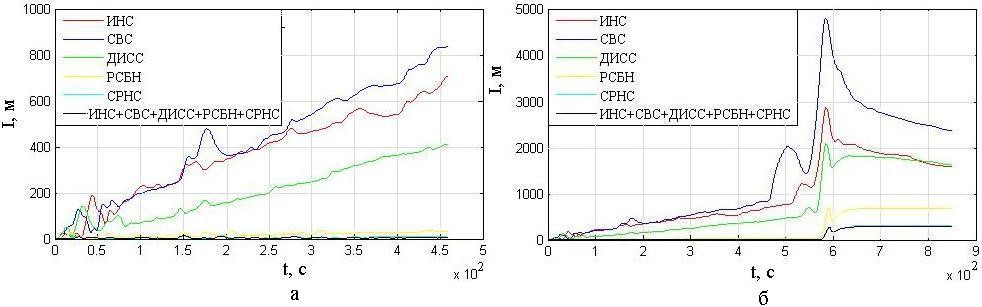
Рис. 5. Зависимость накопленного отклонения от результатов комплексирования систем навигации при полете:
а – по прямой; б – по маршруту
Fig. 5. The dependence of the accumulated deviation I on the results of the integration of navigation systems during flight: a – in a straight line, б – along the route
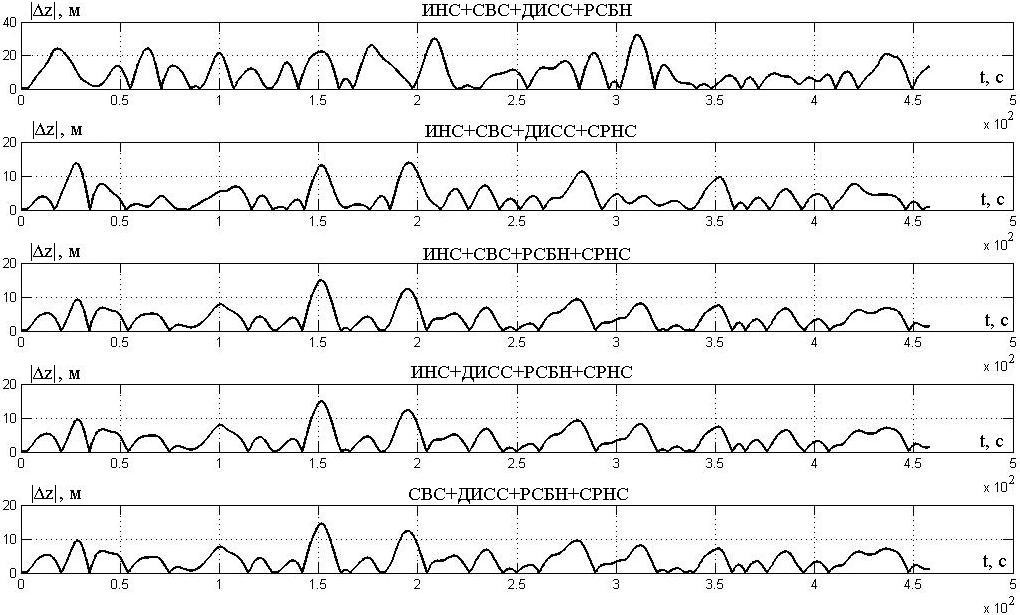
Рис. 6. Абсолютные отклонения траектории полета от ЛЗП
Fig. 6. Absolute deviations of the flight path from the course line (required track)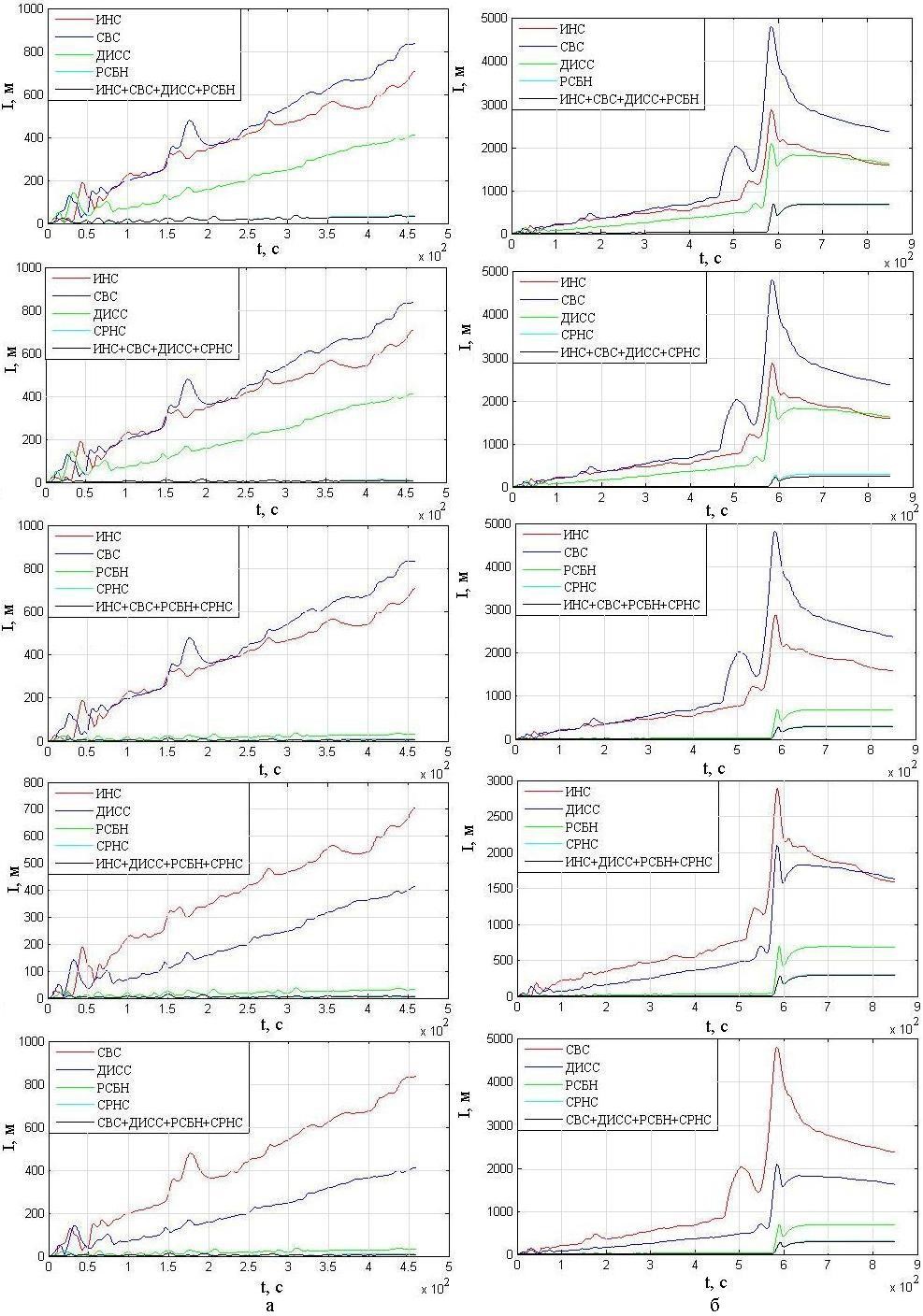
Рис. 7. Влияние комплексирования различных четырех систем на при полете:
а – по прямой; б – по маршруту
Fig. 7. The influence of integrating various four systems on I during flight:
a – in a straight line; б – along a route
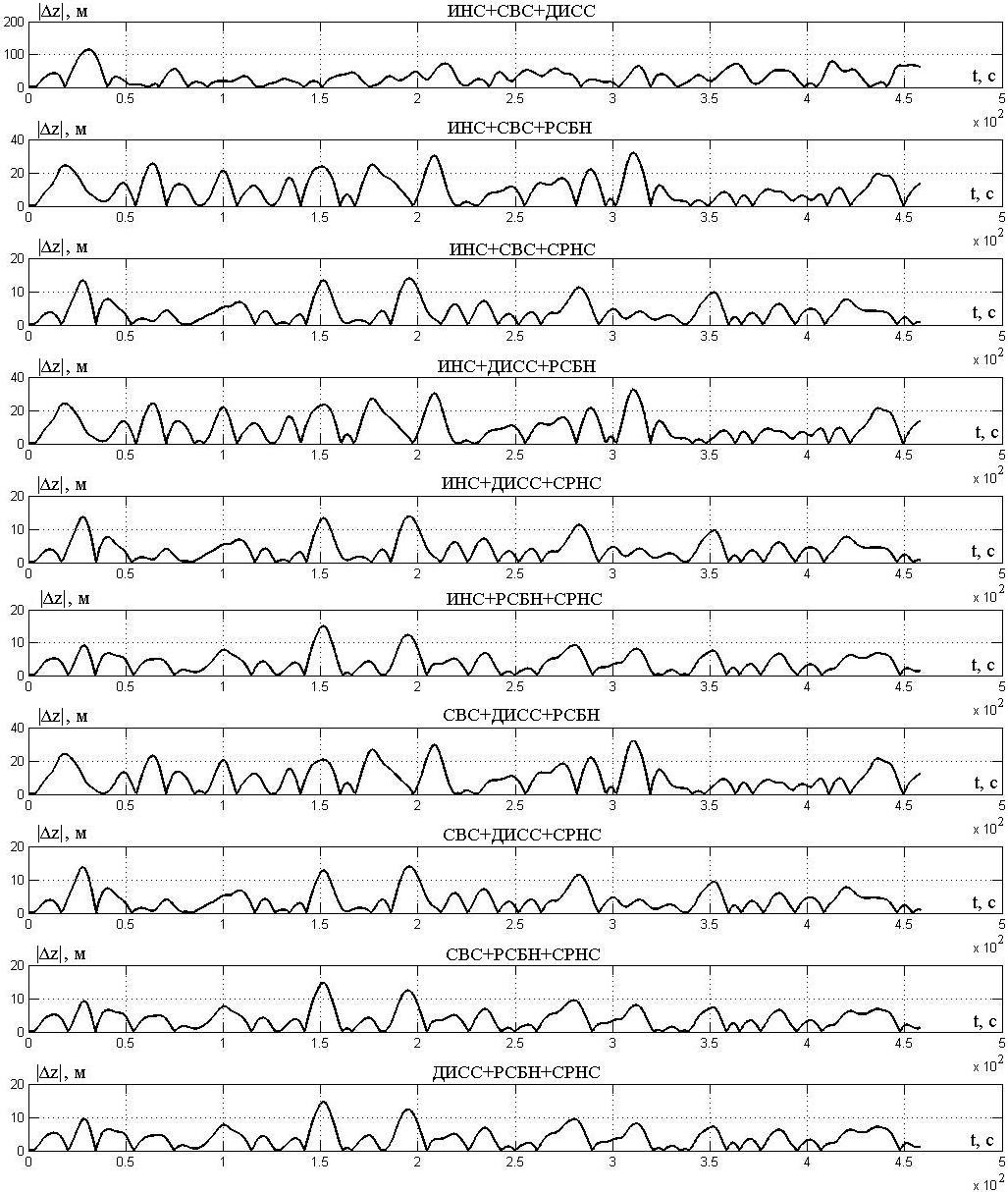
Рис. 8. Результаты определения абсолютного отклонения траектории полета от ЛЗП
при комплексировании трех систем
Fig. 8. The results of determining the absolute deviation of the flight path
from the course line (required track) during integration of 3 system
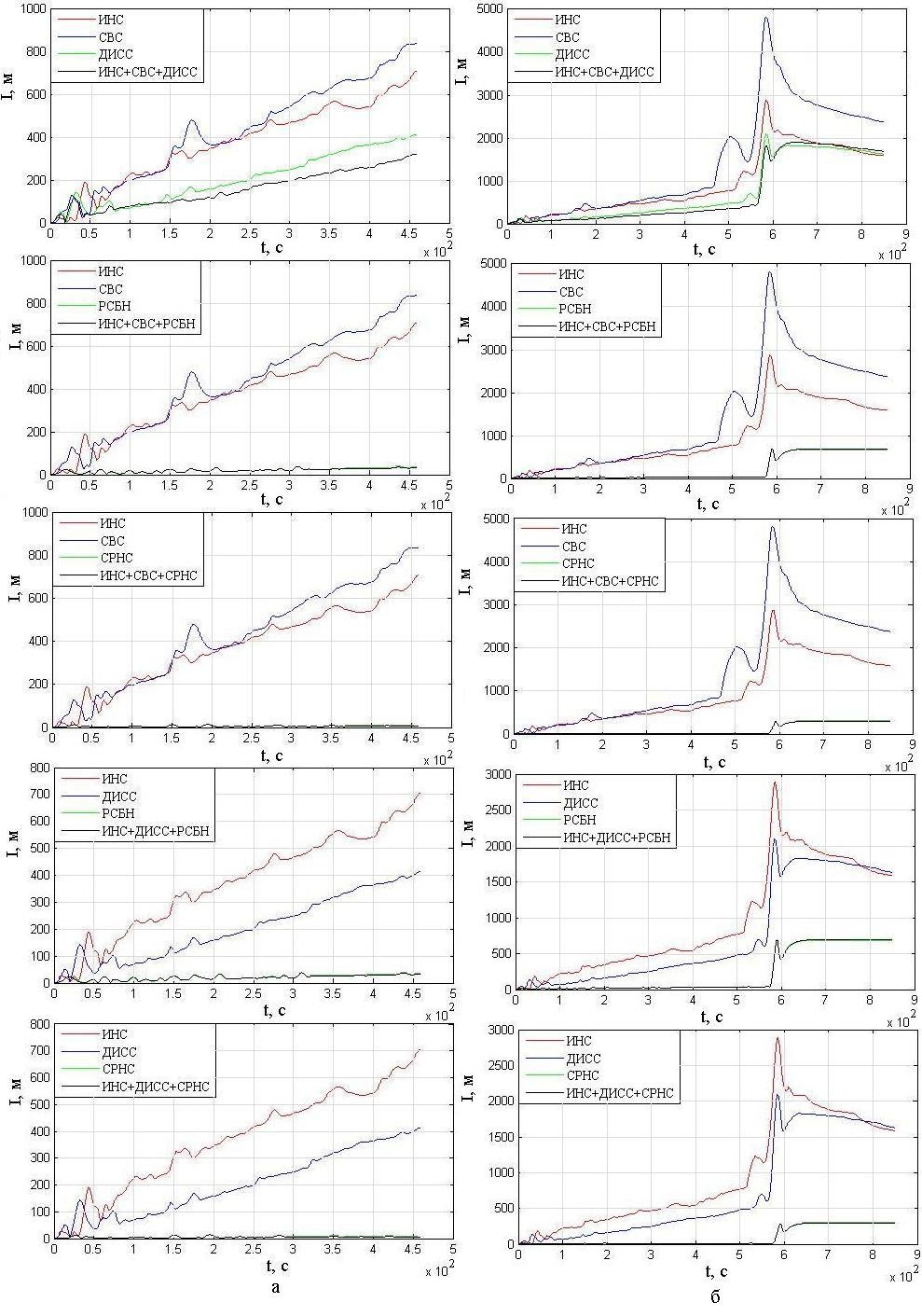
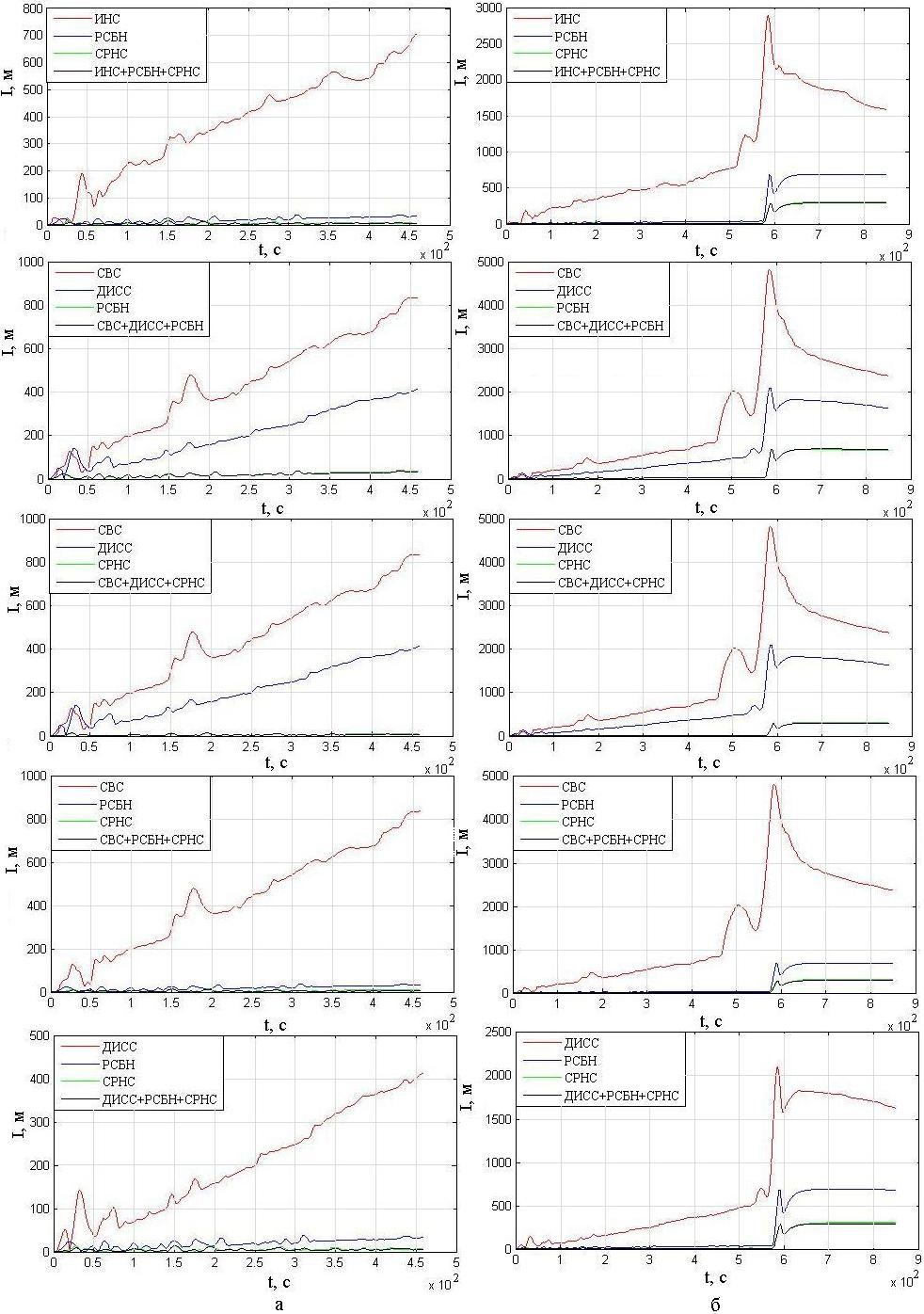
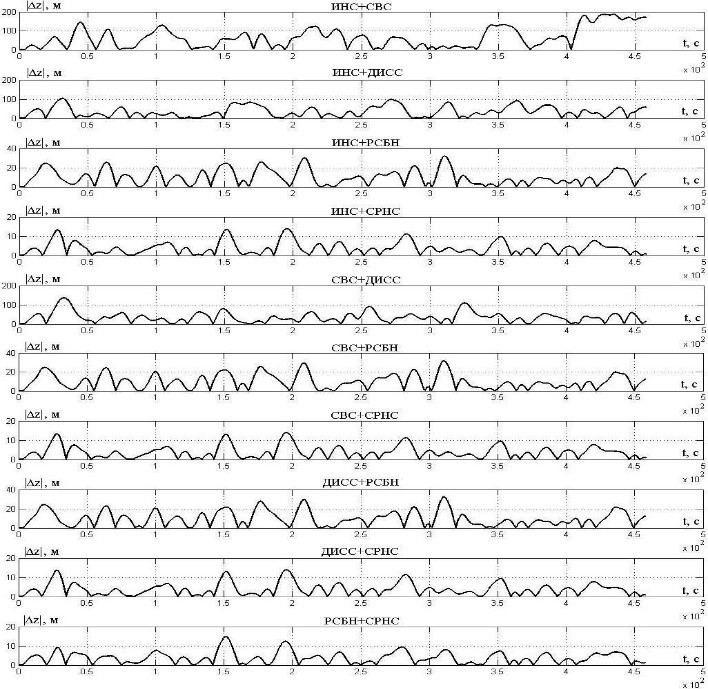
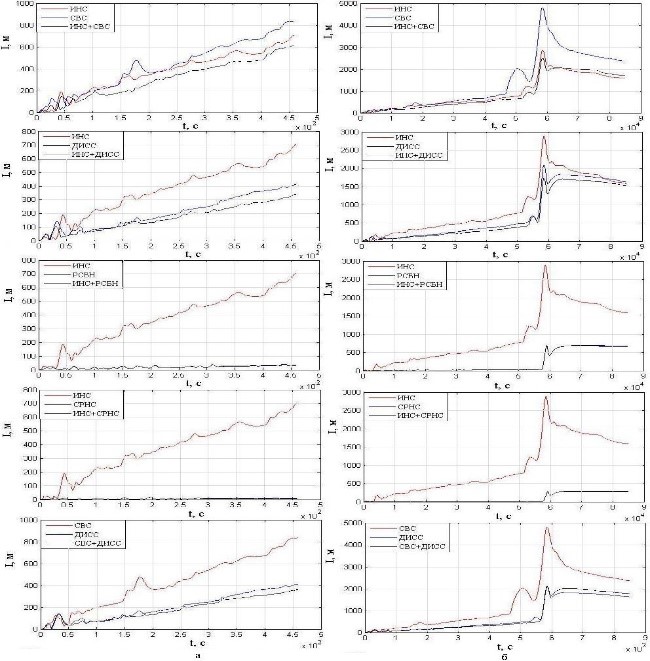
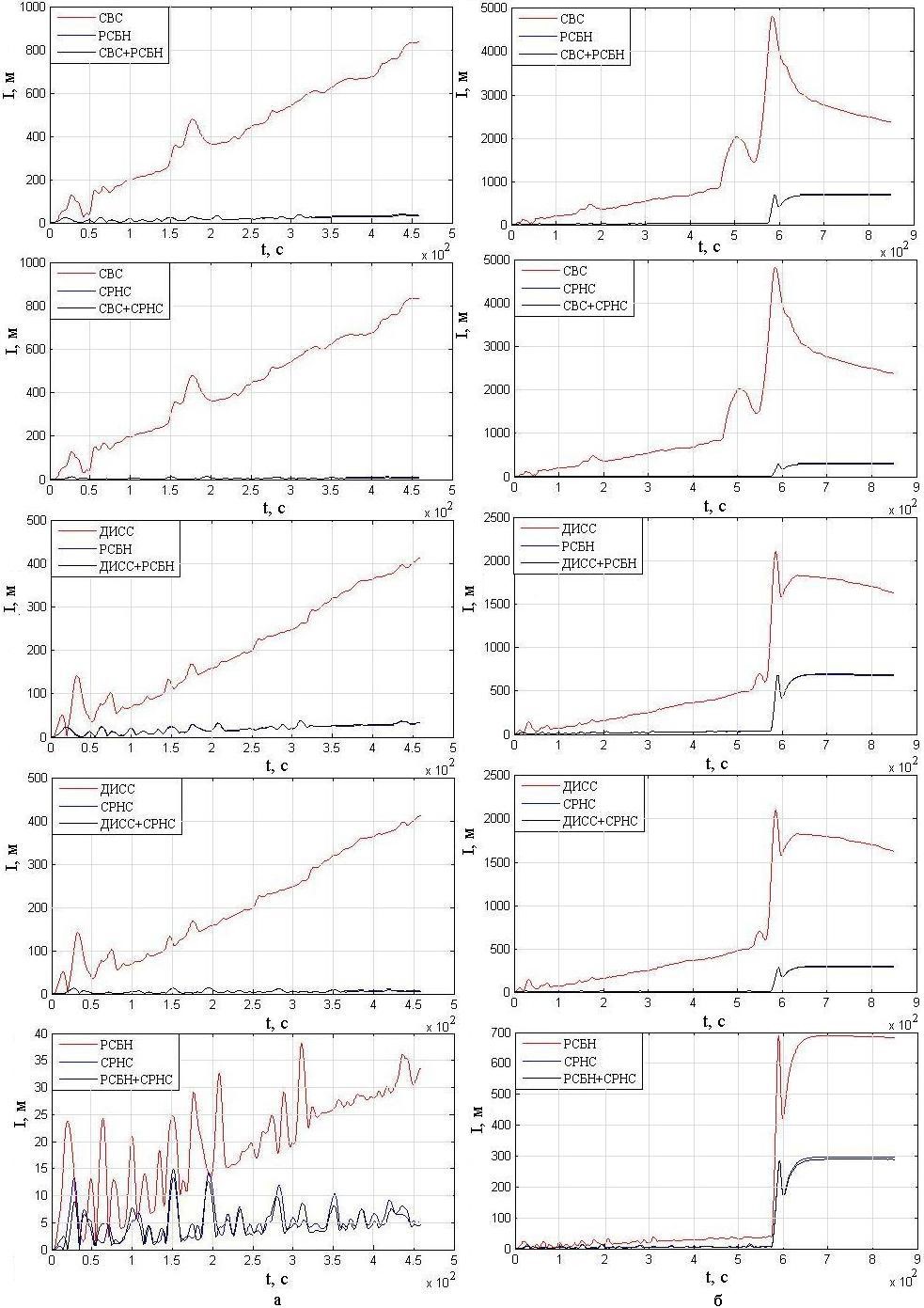
Таблица 2
Table 2
Вероятность удержания ВС в пределах допустимого коридора (200 м)
The probability of keeping the aircraft within the acceptable range (200 m)
|
Навигационная система/комбинация |
Среднеквадратическое отклонение |
Вероятность
|
|
ИНС |
862,14 |
0,2321 |
|
СВС |
2 188,58 |
0,0914 |
|
ДИСС |
416,30 |
0,4812 |
|
РСБН |
33,97 |
0,9999 |
|
СРНС |
18,07 |
0,9999 |
|
Комплексирование всех систем |
12,35 |
0,9999994 |
|
Комплексирование (ИНС, ДИСС, РСБН, СРНС) |
14,21 |
0,9999990 |
|
Комплексирование (ДИСС, РСБН, СРНС) |
15,83 |
0,9999987 |
|
Комплексирование (РСБН, СРНС) |
16,94 |
0,9999983 |
6. Математический анализ причин повышения точности при комплексировании
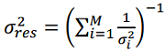 .(17)
.(17) 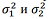 получаем
получаем 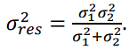 .(18)
.(18)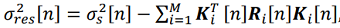 , (19)
, (19) 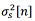 – априорная дисперсия вектора состояния, Ki [n] – коэффициент усиления фильтра для i-й системы, Ri [n] – ковариационная матрица измерений i-й системы.
– априорная дисперсия вектора состояния, Ki [n] – коэффициент усиления фильтра для i-й системы, Ri [n] – ковариационная матрица измерений i-й системы.7. Заключение
Список литературы
1. Петраш В.Я. Методы и модели автоматизированного проектирования летательных аппаратов: учеб. пособие. М.: Изд-во МАИ, 2007. 92 с.
2. Blomenhofer H. Accuracy, Integrity and availability of GLS-based autopilot coupled aircraft landings // NAVIGATION: Journal of the Institute of Navigation. 1996. Vol. 43, iss. 4. Pp. 420–436. DOI: 10.1002/j.2161-4296.1996.tb 01930.x
3. Виндекер А.В., Парафесь С.Г. Выбор конструкционного материала и внешней геометрии газового руля системы склонения беспилотного летательного аппарата // Научный вестник МГТУ ГА. 2018. Т. 21, № 1. С. 67–76. DOI: 10.26467/2079-0619-2018-21-1-67-76
4. Маркелов В.В. Реализация построения маршрутных траекторий для отображения на бортовых многофункциональных индикаторах / В.В. Маркелов, М.О. Костишин, И.О. Жаринов, В.А. Нечаев // Информационно-управляющие системы. 2016. № 1 (80). C. 40–49. DOI: 10.15217/issn1684-8853.2016.1.40
5. Петраш В.Я. Особенности автоматизированного проектирования беспилотных летательных аппаратов с аэрогазодинамическим управлением. М.: Изд-во МАИ-ПРИНТ, 2009. 95 с.
6. Петраш В.Я. Баллистическое и массово-геометрическое проектирование беспилотных ЛА в учебной САПР: учеб. пособие. М.: Изд-во МАИ, 2020. 98 с.
7. Яковлев Г.А., Масальцева Е.К. Моделирование траектории полета ракеты с вертикальным пуском // Техника XXI века глазами молодых ученых и специалистов. 2018. № 17. С. 393–402.
8. Chen Q. Comparison of different k-ε models for indoor air flow computations // Numerical Heat Transfer. 1995. Vol. 28, no. 3. Pp. 353–369. DOI: 10.1080/10407799508928838
9. Du W., Zhou H., Chen W. Trajectory optimization for agile-turn of vertically launched missile // 2016 IEEE International Conference on Mechatronics and Automation, 2016. Pp. 2110–2115. DOI: 10.1109/ICMA.2016.755 8892
10. Маркелов В.В., Костишин М.О., Шукалов А.В. Коррекция курса инерциальной навигационной системы до взлета самолета по информации от спутниковой навигационной системы // Информационно-управляющие системы. 2015. № 6 (79). С. 34–39. DOI: 10.15217/issn1684-8853.2015.6.34
11. Ma H.Y., Cheng P.F., Huang H.D. Research on the complete integrated GPS/INS navi¬ga¬tion system of velocity and attitude // Bulletin of Surveying and Mapping. 2016. No. 3. Pp. 10–14.
12. Murty C., Chakraborty D. Numerical characterisation of jet-vane based thrust vectorcontrol systems // Defence Science Journal. 2015. Vol. 65, no. 4. Pp. 261–264. DOI: 10.14 429/dsj.65.7960
13. Murty C., Rao M.S., Chakraborty D. Numerical simulation of nozzle flow field with jet-vane based thrust vector control [Электронный ресурс] // Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering. 2010. Vol. 224, no. 5. Pp. 541–548. DOI: 10.1243/09544100JAERO677 (дата обращения: 15.08.2024).
14. Tan X., Jian W., Han H. SVR aided adaptive robust filtering algorithm for GPS/INS integrated navigation // Acta Geodaetica et Cartographica Sinica. 2014. Vol. 43, no. 6. Pp. 590–606. DOI: 10.13485/j.cnki.11-2089.2014.0093
15. Tekin R., Atesoglu O., Leblebici-oglu K. Flight control algorithms for a vertical launch air defense missile // Advances in Aerospace Guidance, Navigation and Control / Под ред. Q. Chu, B. Mulder, D. Choukroun, E.J.van Kampen, C. de Visser, G. Looye. Berlin, Heidelberg: Springer, 2013. Pp. 73–84. DOI: 10.10 07/978-3-642-38253-6_6
16. Yogesh M., Hari Rao A.N. Solid particle erosion response of fiber and particulate filled polymer based hybrid composites: a review // Journal of Engineering Research and Applications. 2016. Vol. 6, iss. 1. Pp. 25–39.
17. Jiang C., Zhang S.B., Zhang Q.Z. Adaptive estimation of multiple fading factors for GPS/INS integrated navigation systems [Электронный ресурс] // Sensors. 2017. Vol. 17, iss. 6. ID: 1254. DOI: 10.3390/s17061 254 (дата обращения: 15.08.2024).
Об авторах
А. С. ЗасухинРоссия
Засухин Александр Сергеевич, начальник учебно-тренажерного центра, старший преподаватель кафедры двигателей летательных аппаратов МГТУ ГА
Москва
В. Д. Будаев
Россия
Будаев Владислав Дмитриевич, старший преподаватель кафедры двигателей летательных
аппаратов МГТУ ГА
Москва
Д. О. Сизиков
Россия
Сизиков Даниил Олегович, старший преподаватель кафедры технической эксплуатации авиационных электросистем и пилотажно-навигационных комплексов МГТУ ГА
Москва
Рецензия
Для цитирования:
Засухин А.С., Будаев В.Д., Сизиков Д.О. Исследование эффективности алгоритмов комплексирования навигационных систем на основе расширенного фильтра Винера. Научный вестник МГТУ ГА. 2025;28(5):22-40. https://doi.org/10.26467/2079-0619-2025-28-5-22-40
For citation:
Zasukhin A.S., Budaev V.D., Sizikov D.O. The study of the efficiency of navigation system integration algorithms based on the extended Wiener filter. Civil Aviation High Technologies. 2025;28(5):22-40. https://doi.org/10.26467/2079-0619-2025-28-5-22-40



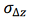 , м
, м





































