Перейти к:
Метод расчета устойчивости обшивок хвостовых отсеков лопастей несущего винта под действием ветра на стоянке вертолета
https://doi.org/10.26467/2079-0619-2025-28-5-63-75
Аннотация
В связи с растущей необходимостью эксплуатации вертолетов в местах с ветрами высокой интенсивности существующие подходы к проектированию лопастей несущего винта (ЛНВ) должны быть пересмотрены на предмет полноты учета расчетных случаев ветрового нагружения. Большую часть времени в эксплуатации вертолет находится на стоянке, а лопасти подвергаются ветровому воздействию, способному приводить к повреждениям, препятствующим возможности их дальнейшей эксплуатации. В частности, известны случаи появления гофров и отслоений обшивок хвостовых отсеков лопастей от заполнителей. В случае превышения установленных в эксплуатационной документации допусков на размеры указанных дефектов хвостовые отсеки либо ремонтируются, либо заменяются на заводе – изготовителе лопастей. В настоящей работе рассмотрена задача устойчивости композитных обшивок хвостовых отсеков невращающихся ЛНВ, нагружаемых ветровым потоком. Расчетная схема моделируемых обшивок соответствует ортотропной прямоугольной пластине, закрепленной на упругом основании и нагруженной по стороне ее сопряжения с лонжероном лопасти. Напряженно-деформированное состояние (НДС) обшивки определяется из решения плоской задачи теории упругости для пластины, расчетные нагрузки для которой в соответствии с условием совместности деформаций лонжерона ЛНВ и обшивки определяются в результате решения задачи ветрового нагружения лопасти в целом. В работе выведено дифференциальное уравнение устойчивости ортотропной пластины на упругом основании, моделирующее обшивку хвостового отсека ЛНВ. Получено выражение для расчета критических напряжений, соответствующих началу возникновения местной потери устойчивости обшивок. Из условия проявления местной потери устойчивости обшивок вычислена предельная скорость ветра для ЛНВ вертолета типа Ми-38.
Ключевые слова
Для цитирования:
Каргаев М.В. Метод расчета устойчивости обшивок хвостовых отсеков лопастей несущего винта под действием ветра на стоянке вертолета. Научный вестник МГТУ ГА. 2025;28(5):63-75. https://doi.org/10.26467/2079-0619-2025-28-5-63-75
For citation:
Kargaev M.V. Method of stability computation of the main rotor blades tail section skins subject to wind at a helicopter parking lot. Civil Aviation High Technologies. 2025;28(5):63-75. (In Russ.) https://doi.org/10.26467/2079-0619-2025-28-5-63-75
Введение
Процесс проектирования лопастей несущего винта вертолета включает в себя этапы по выбору параметров хвостовых отсеков. Как установлено в работе [1], при выборе данных параметров помимо полетных случаев нагружения [2][3] необходимо учитывать и наземные случаи нагружения. Одним из них является ветровое нагружение, характеристики которого должны быть заданы в техническом задании на проектируемую лопасть. Анализ напряженно-деформированного состояния обшивок хвостовых отсеков невращающейся лопасти под действием ступенчатого порыва ветра [1] показал, что действующие вдоль задней стенки лонжерона сжимающие продольные напряжения в обшивке могут приводить к образованию зоны местной потери устойчивости [4–6]. Недопустимость местной потери устойчивости обшивок обусловлена их сопутствующим отслоением от заполнителя хвостового отсека, при достижении критической величины которого дальнейшая эксплуатация лопасти без восстановительного ремонта становится небезопасной.
Исходя из этого, для рационального выбора параметров хвостовых отсеков на этапе проектирования лопасти необходимо иметь метод, позволяющий выполнять расчет на местную устойчивость обшивок хвостовых отсеков ЛНВ, подверженных воздействию ветра, для чего в данной работе изложен метод, построенный на поочередном расчете напряжений в лонжероне [7] и обшивке [1] лопасти под действием ветра, сравнении полученных напряжений с критическими напряжениями, рассчитанными по формулам, полученным в настоящей работе.
Вывод дифференциального уравнения устойчивости обшивки
Рассмотрим разрезной хвостовой отсек ЛНВ [8], конструктивно образованный склейкой ограниченного по ширине торцевыми нервюрами заполнителя с верхней и нижней обшивками, замыкающимися стрингером (рис. 1). Будем полагать, что нагружение обшивок происходит вследствие деформаций лопасти, к лонжерону которой они приклеены.
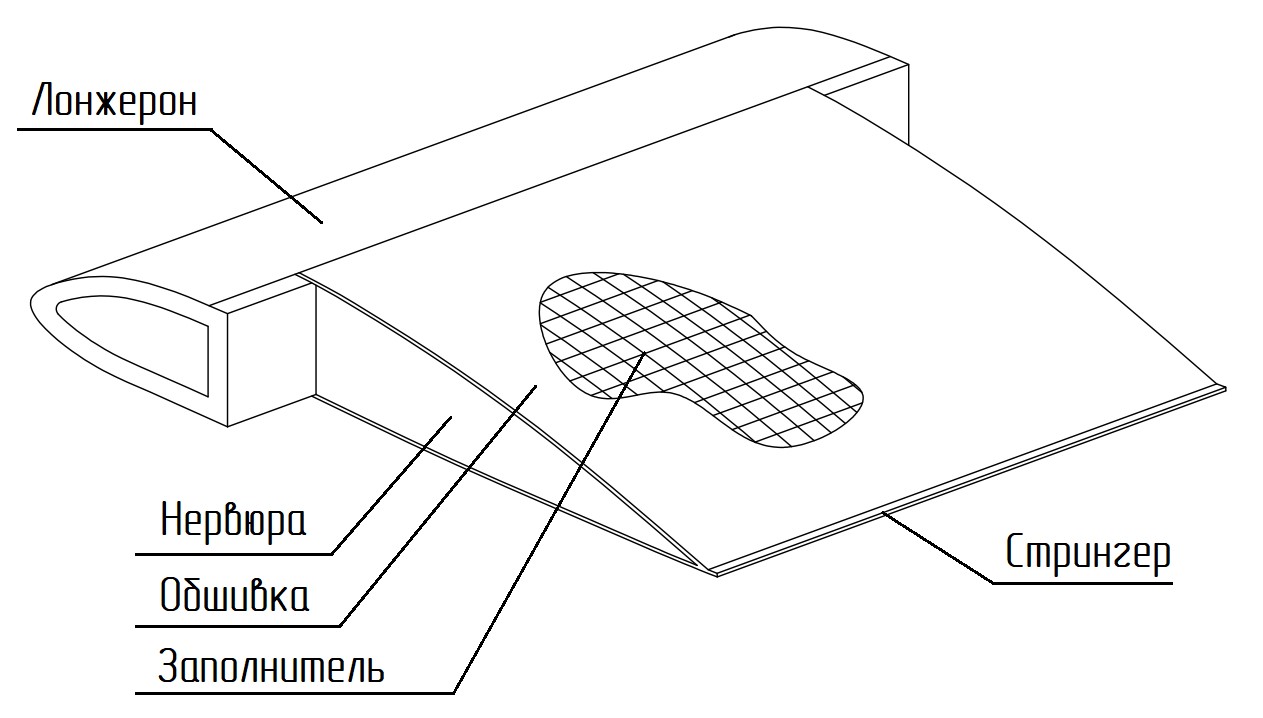
Рис. 1. Конструкция разрезного хвостового отсека лопасти
Fig. 1. Design of the split tail blade section
Для вывода дифференциального уравнения устойчивости обшивки используем систему дифференциальных уравнений, описывающую НДС обшивки рассматриваемого хвостового отсека [1]:
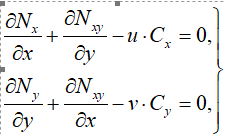 (1)
(1)
где u и v – перемещения пластины по осям Ox и Oy.
В системе (1) перейдем от погонных усилий к напряжениям, выполнив соответствующие замены, используя равенства Nx =σx · δ, Ny = σy · δ, Nxy = τxy · δ, где δ – толщина пластины в рассматриваемой точке, σx и σy – нормальные напряжения по осям Ox и Oy, τxy – напряжения сдвига.
Граничные условия для уравнений (1) представлены на рис. 2 и определяются соотношениями [1]
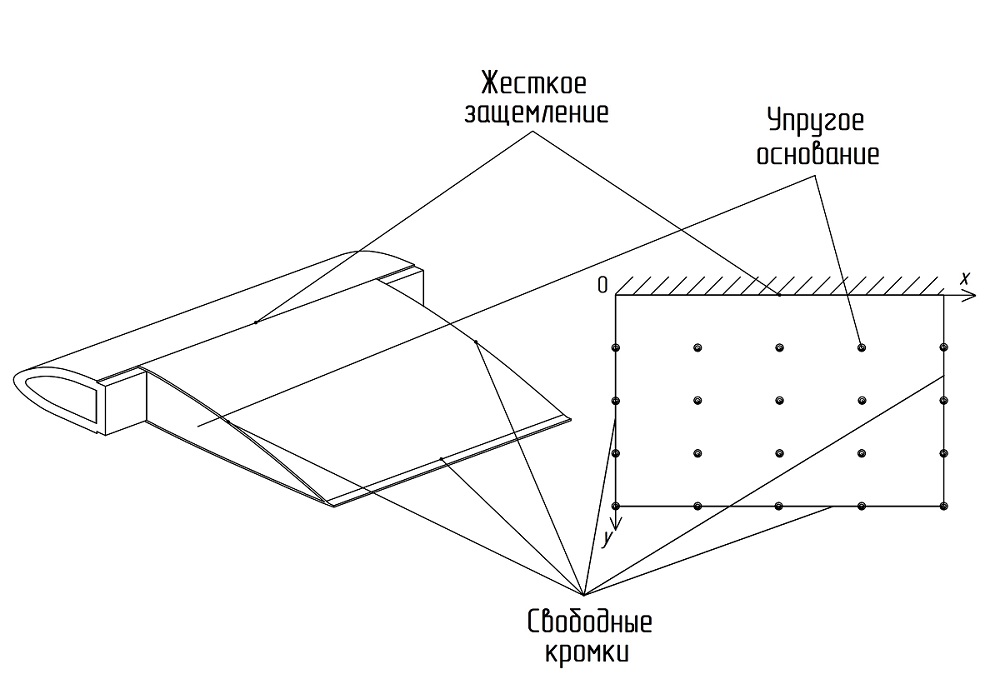
Рис. 2. Граничные условия
Fig. 2. Boundary conditions
при x = 0, L → σx = 0; τxy = 0;
при y = H → σy = 0; τxy = 0;
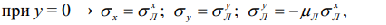
где 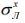 – напряжения в лонжероне в месте приклейки обшивки, обусловленные воздействием ветра [7];
– напряжения в лонжероне в месте приклейки обшивки, обусловленные воздействием ветра [7]; 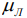 – коэффициент Пуассона лонжерона; L – длина обшивки; H – ширина обшивки. Таким образом, сопряженная с лонжероном грань обшивки имеет совместные с ним деформации, а остальные грани обшивки свободно деформируются. Влияние заполнителя на НДС обшивки в (1) учитывается за счет наличия жесткостей Cx и Cy упругого основания.
– коэффициент Пуассона лонжерона; L – длина обшивки; H – ширина обшивки. Таким образом, сопряженная с лонжероном грань обшивки имеет совместные с ним деформации, а остальные грани обшивки свободно деформируются. Влияние заполнителя на НДС обшивки в (1) учитывается за счет наличия жесткостей Cx и Cy упругого основания.
Получим дифференциальное уравнение устойчивости для ортотропной пластины на упругом основании, исходя из предположения о возможности состояния равновесия пластины в искривленном состоянии. Данное состояние будем характеризовать прогибом w вдоль оси Oz. Допустим, что при изгибе пластины согласно гипотезам Кирхгофа [9][10] будет иметь место отсутствие деформаций поперечного сдвига:
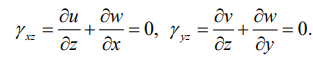 (2)
(2)
Тогда из зависимостей (2), принимая, что точки срединной поверхности перемещаются при изгибе только вдоль оси Oz, можно получить выражения
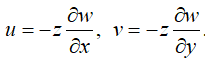
Связь деформаций пластины с перемещениями u и v устанавливается через формулы Коши
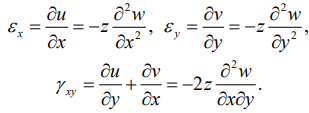 (3)
(3)
Для ортотропной пластины действующие в ее плоскости напряжения с учетом равенства нулю напряжений в направлении оси Oz, то есть σz = 0, определяются зависимостями обобщенного закона Гука в виде [11–13]
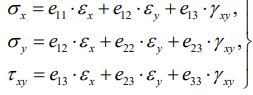 (4)
(4)
Упругие постоянные материала e11, e12, e13, e22, e23, e33 [11–13], составляющие матрицу E коэффициентов жесткости, могут быть получены обращением матрицы податливостей A, то есть E = A−1, которая имеет вид
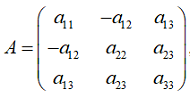
где коэффициенты податливости матрицы A [1] – функции «технических» модулей упругости Ex, Ey, G, μx, ηx, ηy и угла φ ориентировки осей материала относительно расчетных осей Ox и Oy, определяются по формулам
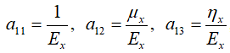 ,
,
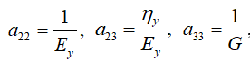
Получим уравнения, связывающие погонные изгибающие и крутящий моменты с прогибом w вдоль оси Oz, для чего сначала подставим формулы (3) в зависимости (4):
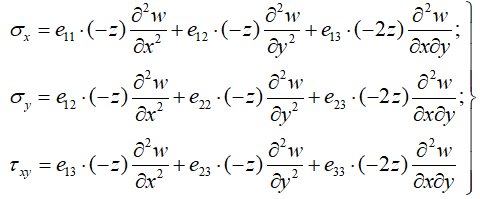 (5)
(5)
Далее перейдем к равнодействующим напряжений (5) по толщине пластины:
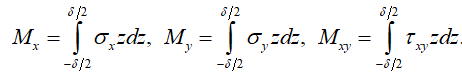 (6)
(6)
Окончательно после интегрирования выражений (6) с учетом (5) получим
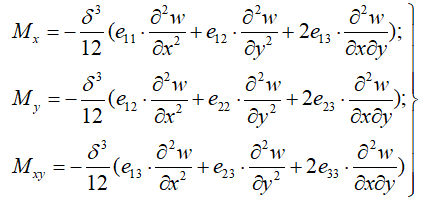 (7)
(7)
Перерезывающие силы Qx и Qy, действующие в сечениях пластины, выражаются через w из уравнения равновесия элемента пластины в проекции на ось Oz [9] [10], которое для условий настоящей задачи имеет вид
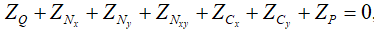 (8)
(8)
где ZQ – проекция перерезывающих сил, а 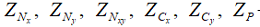 – проекции сил начального состояния. Согласно [9] имеем
– проекции сил начального состояния. Согласно [9] имеем
 (9)
(9)
Аналогично выражениям для 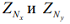 можно получить выражения для
можно получить выражения для 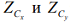 :
:
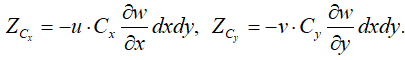 (10)
(10)
Выражение для ΖΡ получим исходя из предположения о том, что заполнитель является легким, а также маложестким в направлении оси Oz, и при потере устойчивости происходит выпучивание несущих слоев – обшивок. При этом роль заполнителя сводится исключительно к работе на сдвиг, то есть обеспечению совместной работы обшивок, воспринимающих продольные силы и моменты. Будем предполагать основание линейно упругим. Тогда давление P, действующее со стороны заполнителя на обшивку, пропорционально ее прогибу w:
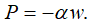 (11)
(11)
Применим закон Гука для столбика заполнителя единичной площади высотой hз нагруженного давлением P, тогда получим выражение для его укорочения, равного прогибу w:
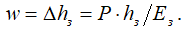 (12)
(12)
Высоту сотового заполнителя hз, как и в [1], примем в виде квадратичной функции, изменяющейся вдоль оси Oy [1]:
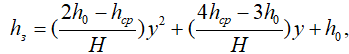 (13)
(13)
где h0 – высота хвостового отсека в месте приклейки к задней стенке лонжерона, hср – высота хвостового отсека посередине ширины хвостового отсека.
Сопоставляя выражения (11) и (12), с учетом (13) получаем, что
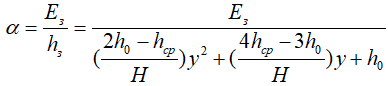
Искомое выражение для  имеет вид
имеет вид
 (14)
(14)
Подставив выражения (9), (10) и (14) в уравнение (8), получим уравнение равновесия элемента пластины
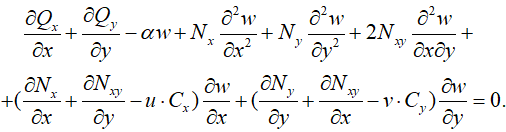 (15)
(15)
Учитывая, что выражения, записанные в скобках уравнения (15), равны нулю в силу соотношений (1), окончательно получим
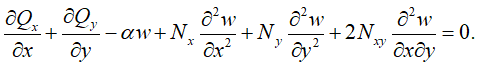 (16)
(16)
Связь между перерезывающими силами и моментами для рассматриваемого случая нагружения пластины определяется уравнениями
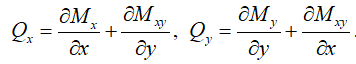 (17)
(17)
Подставив уравнения (17) и (7) в (16), получим дифференциальное уравнение устойчивости ортотропной пластины на упругом основании:
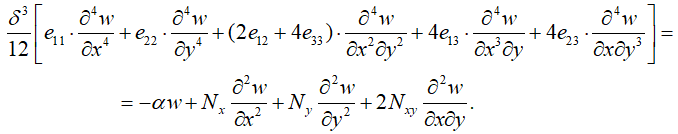 (18)
(18)
Определение критических напряжений, соответствующих местной потере устойчивости обшивки
При решении задачи о потере устойчивости пластины предполагается, что до потери устойчивости она является плоской [13]. В таком случае все силы, действующие на пластину, действуют по ее срединной поверхности и при деформациях пластины не изменяются ни по величине, ни по направлению. То есть докритическое напряженное состояние пластины является плоским.
Будем полагать, что докритические силы и перемещения для рассматриваемой задачи определяются из решения уравнений (1) методом [1], основанным на применении метода сеток [10][14].
В таком случае задача нахождения критических напряжений местной потери устойчивости должна решаться для элементарной прямоугольной пластинки, жестко защемленной по сторонам размерами li и hj, полученной путем разбиения расчетной области обшивки ортогональной сеткой (i – номер узла сетки по оси Oy, j – номер узла по оси Ox). Далее индексы i и j всюду, за исключением некоторых выражений, для удобства восприятия опущены. Расчетная область обшивки [1] представлена на рис. 3.

Рис. 3. Расчетная область обшивки хвостового отсека
Fig. 3. Computational domain of the tail section skin
По найденным в результате решения системы уравнений (1) перемещениям u и v определяются действующие в обшивке напряжения σx, σy и τxy. Для определения критических напряжений местной потери устойчивости удобно перейти от рассмотрения плоского напряженного состояния, определяемого напряжениями σx, σy и σxy, к главным напряжениям σξ и ση, определяемым по формулам [15]
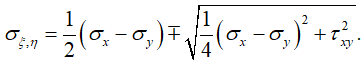
Ориентация главных напряжений относительно системы координат Oxy определяется поворотом исходной на угол:
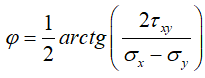
Тогда в рассматриваемой задаче на каждую пластинку действуют распределенные по ее краям сжимающие усилия Nξ = δ · σξ и растягивающие усилия Nη = δ · ση.
Таким образом, уравнение местной потери устойчивости (18) примет вид
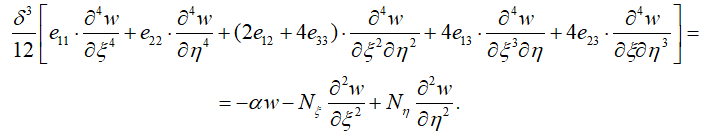 (19)
(19)
Для определения критических напряжений из уравнения (19) используем метод Бубнова – Галеркина [16]. Функция прогибов пластины должна удовлетворять граничным условиям жесткого защемления по контуру. В качестве аппроксимирующих функций w могут применяться простые ортогональные [17] и неортогональные полиномы [18][19] или тригонометрические ряды [20]. Зададим функцию прогибов w в виде
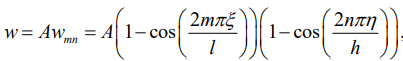 (20)
(20)
где m и n – числа полуволн косинусоид в направлениях ξ и η соответственно при потере устойчивости (m = 1, 2, 3, …; n = 1, 2, 3, …); А – произвольная постоянная.
Тогда в соответствии с методом Бубнова – Галеркина должно выполняться равенство
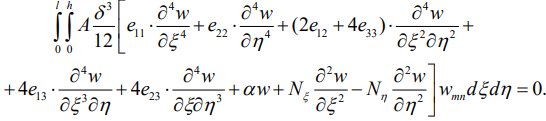 (21)
(21)
Подставив в уравнение (21) функцию прогибов в виде (20), получим равенство
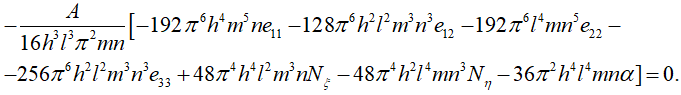 (22)
(22)
Для существования отличных от нуля решений выражение, стоящее в квадратных скобках (22), должно обращаться в нуль. Это условие приводит к уравнению для оценки критического сжимающего усилия:
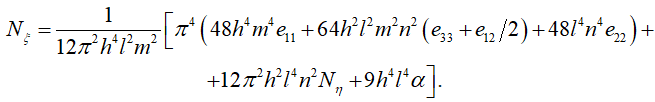 (23)
(23)
Задаваясь различными целыми значениями m и n, при известной величине Nη, имеем множество значений Nξ, удовлетворяющих равенству (23). В качестве критического будем рассматривать наименьшее усилие Nξ, при котором все еще возможно равновесие пластины в искривленном состоянии. Из рассмотрения (23) видно, что минимум Nξ достигается в случае n = 1. Это означает, что при потере устойчивости в направлении η всегда будет образовываться одна полуволна. Тогда уравнение (23) можно представить в виде
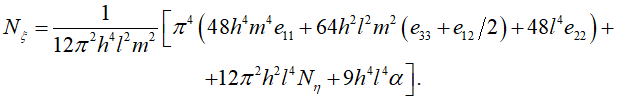 (24)
(24)
Минимальное значение усилия (24) определим из условия
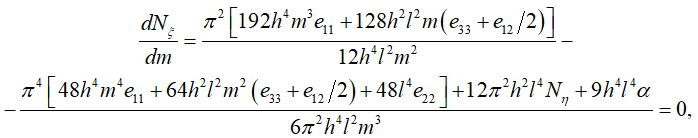
которое приводит к значению
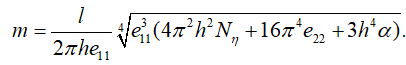 (25)
(25)
Подставив (25) в (24), а также учитывая, что Nξ = δ · σξ, а Nη = δ · ση, получим окончательное выражение для расчета критического напряжения в обшивке:
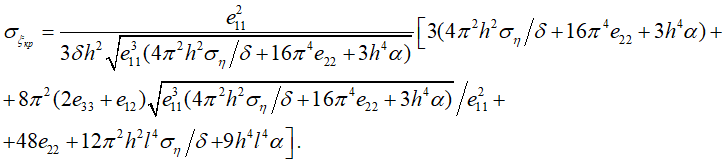 (26)
(26)
По сложившейся практике [15], если второе главное напряжение ση растягивающее, то оно обычно игнорируется, в этом случае из (26) имеем
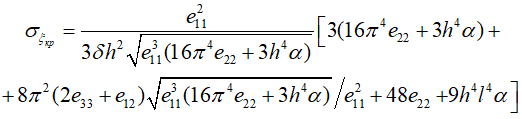 (27)
(27)
Результаты численных расчетов
Далее представлены результаты вычислений коэффициентов запаса устойчивости kV, выполненных с использованием полученных выражений (26) и (27) для расчета критических напряжений 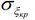 местной потери устойчивости обшивки хвостового отсека лопасти при действии различных скоростей ветра Vв при угле атаки –10° и угле скольжения 0°, при постоянных величинах шагов разбиения расчетной области обшивки вдоль оси Ox и оси Oy, то есть при li = l и hj = h. Данные условия ветрового нагружения использованы для иллюстрации расчетов по определению предельных скоростей ветра из условия местной потери устойчивости обшивки и не являются критическими. Методика выбора критического направления обдува изложена в статье [7].
местной потери устойчивости обшивки хвостового отсека лопасти при действии различных скоростей ветра Vв при угле атаки –10° и угле скольжения 0°, при постоянных величинах шагов разбиения расчетной области обшивки вдоль оси Ox и оси Oy, то есть при li = l и hj = h. Данные условия ветрового нагружения использованы для иллюстрации расчетов по определению предельных скоростей ветра из условия местной потери устойчивости обшивки и не являются критическими. Методика выбора критического направления обдува изложена в статье [7].
Напряжения в лонжероне лопасти, нагружаемой ветровым потоком, определены по методу [7]. Расчет критических напряжений местной потери устойчивости  и соответствующих им коэффициентов запаса kV выполнен, как показано в [1], для наиболее нагруженного хвостового отсека модельной лопасти вертолета типа Ми-38, расположенного на удалении 5,45–5,85 м. Это позволяет установить предельную скорость ветра для лопасти, соответствующую началу возникновения местной потери устойчивости обшивок. Поскольку растягивающие напряжения ση имеют отличные значения в различных точках обшивки, то расчет ее устойчивости удобно вести, используя коэффициент запаса kV, определяемый максимумом отношения сжимающих напряжений σξ и критических напряжений
и соответствующих им коэффициентов запаса kV выполнен, как показано в [1], для наиболее нагруженного хвостового отсека модельной лопасти вертолета типа Ми-38, расположенного на удалении 5,45–5,85 м. Это позволяет установить предельную скорость ветра для лопасти, соответствующую началу возникновения местной потери устойчивости обшивок. Поскольку растягивающие напряжения ση имеют отличные значения в различных точках обшивки, то расчет ее устойчивости удобно вести, используя коэффициент запаса kV, определяемый максимумом отношения сжимающих напряжений σξ и критических напряжений 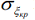 для расчетной области обшивки, то есть
для расчетной области обшивки, то есть 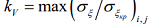 . Зависимость коэффициента запаса kV, характеризующая момент возникновения местной потери устойчивости для наиболее нагруженной обшивки хвостового отсека ЛНВ, от скорости ветра Vв приведена на рис. 4.
. Зависимость коэффициента запаса kV, характеризующая момент возникновения местной потери устойчивости для наиболее нагруженной обшивки хвостового отсека ЛНВ, от скорости ветра Vв приведена на рис. 4.
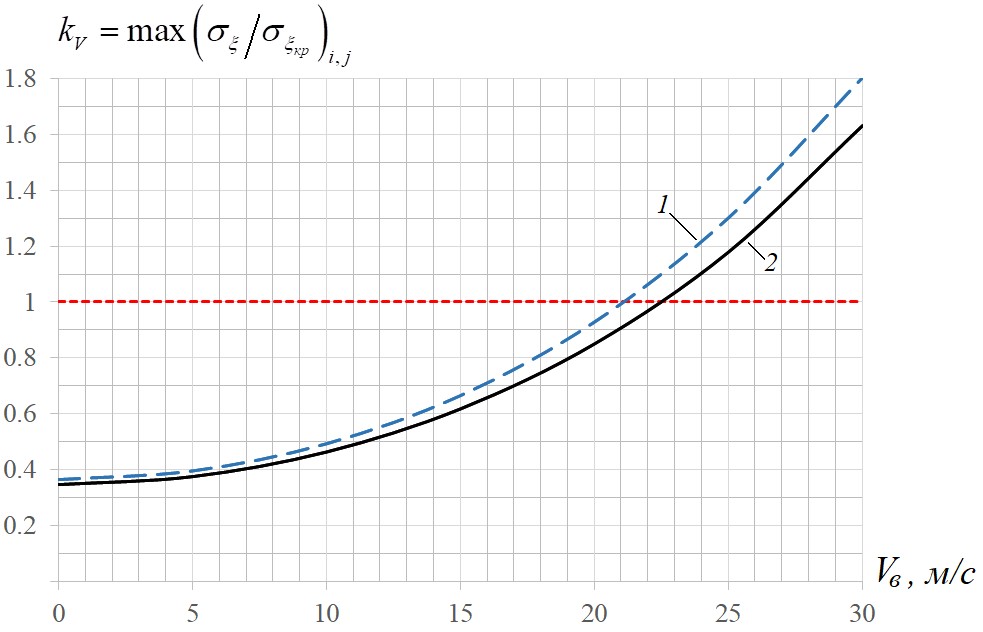
Рис. 4. Зависимость коэффициента запаса от скорости ветра: 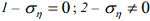
Fig. 4. Dependence of the reserve coefficient on wind speed: 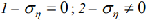
Необходимо отметить, что число полуволн m, вычисляемое по формуле (25), должно иметь целое значение. Это достигается за счет подбора величин шагов разбиения расчетной области вдоль оси Ox и оси Oy, то есть l и h.
Комбинация сжимающих продольных напряжений σx, а также растягивающих и касательных напряжений σsy и txy соответственно, как следует из сопоставления зависимостей, приведенных на рис. 4, при предельных скоростях ветра может приводить к появлению зоны местной потери устойчивости обшивки расположенной вдоль задней стенки лонжерона. При этом расчет при 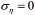 дает более консервативную оценку. Из рис. 4 также следует, что предельная скорость ветра для заданного направления действия ветра имеет значение, равное 21,1 м/с при
дает более консервативную оценку. Из рис. 4 также следует, что предельная скорость ветра для заданного направления действия ветра имеет значение, равное 21,1 м/с при 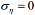 и 22,5 м/с при
и 22,5 м/с при 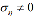 , что несколько меньше полученной в [1] предельной скорости 26 м/с по условию прочности обшивок от действия растягивающих напряжений.
, что несколько меньше полученной в [1] предельной скорости 26 м/с по условию прочности обшивок от действия растягивающих напряжений.
Заключение
Установленная для рассматриваемой лопасти несущего винта предельная скорость ветра 22,5 м/с по условию начала местной потери устойчивости обшивок хвостовых отсеков оказалась меньше предельной скоростью ветра 26 м/с, вычисленной по условию прочности обшивок от действия растягивающих напряжений. При этом с практической точки зрения это не означает, что по данному критерию необходимо ограничивать допустимую в эксплуатации скорость ветра значением 22,5 м/с, поскольку данное значение может быть увеличено как за счет введения допуска на площадь отслоения обшивки от заполнителя, так и за счет допущения о возможности ремонта или замены поврежденного хвостового отсека в эксплуатации вертолета.
Исходя из этого, процесс выбора параметров хвостовых отсеков ЛНВ должен включать оба расчетных случая ветрового нагружения, а именно расчеты на статическую прочность и устойчивость обшивок, по результатам которых должна быть определена предельно допустимая в эксплуатации скорость ветра как наименьшая из полученных по разным критериям.
Список литературы
1. Каргаев М.В., Савина Д.Б. Метод расчета напряжений в обшивке хвостовых отсеков невращающихся лопастей несущего винта под действием ветра на стоянке вертолета // Вестник Московского авиационного института. 2023. Т. 30, № 3. С. 17–25.
2. Johnson W. Rotorcraft aeromechanics. NY: Cambridge University Press, 2013. 944 p.
3. Richard L.B. Rotary wing structural dynamics and aeroelasticity. Washington, AIAA, DC, 2005. 584 p.
4. Орешко Е.И. Обзор критериев прочности материалов / Е.И. Орешко, В.С. Ерасов, А.В. Гриневич, П.В. Шершак // Труды ВИАМ. 2019. № 9 (81). С. 108–126. DOI: 10.18577/2307-6046-2019-0-9-108-126
5. Гришин В.И., Дзюба А.С., Дударьков Ю.И. Прочность и устойчивость элементов и соединений авиационных конструкций из композитов. М.: Физматлит, 2013. 272 с.
6. Смердов А.А. Возможности повышения местной устойчивости подкрепленных и интегральных композитных конструкций // Известия высших учебных заведений. Машиностроение. 2014. № 10 (655). С. 70–79.
7. Каргаев М.В. Расчет напряжений в лопасти несущего винта вертолета на базе нелинейной модели нагружения при статическом воздействии ветра // Вестник Московского авиационного института. 2019. Т. 26, № 2. С. 34–42.
8. Дудник В.В. Конструкция вертолетов. Ростов н/Д: Издательский дом ИУИ АП, 2005. 158 с.
9. Савельев Л.М. Устойчивость конструкций: конспект лекций. Самара: СГАУ, 2013. 77 с.
10. Ефимов В.В. Динамика и прочность авиационных конструкций. Часть 1: учеб. пособие. М.: МГТУ ГА, 2013. 72 с.
11. Лехницкий С.Г. Теория упругости анизотропного тела. 2-е изд. М.: Наука, 1977. 416 с.
12. Ашкенази Е.К., Ганов Э.В. Анизотропия конструкционных материалов: справочник. 2-е изд., перераб. и доп. Л.: Машиностроение, 1980. 248 с.
13. Гарифуллин М.Ф., Казаков И.А., Киреев В.А. Анализ устойчивости тонких композитных пластин при различных вариантах граничных условий // Ученые записки ЦАГИ. 2024. Т. 55, № 4. С. 83–94.
14. Мазо А.Б. Вычислительная гидродинамика. Часть 1. Математические модели, сетки и сеточные схемы: учеб. пособие. Казань: Казан. ун-т, 2018. 165 с.
15. Муйземнек А.Ю., Карташова Е.Д. Механика деформирования и разрушения полимерных слоистых композиционных материалов: учеб. пособие. Пенза: Изд-во ПГУ, 2017. 56 с.
16. Колмогоров Г.Л., Мельникова Т.Е., Азина Е.О. Применение метода БубноваГалеркина для оценки устойчивости анизотропных пластин // Строительная механика инженерных конструкций и сооружений. 2017. № 4. С. 29–33. DOI: 10.22363/1815-5235-2017-4-29-33
17. Moreno-Garcia P., Araujo dos Santos J.V., Lopes H. A review and study on Ritz method admissible functions with emphasis on buckling and free vibration of isotropic and anisotropic beams and plates // Archives of Computational Methods in Engineering. 2017. Vol. 25. Pp. 785–815. DOI: 10.1007/s11831-017-9214-7
18. Гарифуллин М.Ф., Казаков И.А., Киреев В.А. Приближенный метод анализа устойчивости композитных пластин с малоразмерными вырезами // Ученые записки ЦАГИ. 2024. Т. 55, № 5. С. 81–89.
19. Bao S.Y., Cao J.R. Elastic buckling analysis of rectangular plates with arbitrary elastic boundary conditions // Chinese Journal of Ship Research. 2020. Vol. 15, no. 6. Pp. 162–169. DOI: 10.19693/j.issn.1673-3185.01808
20. Lampros P., Christos K. Shear buckling of rectangular plates with two concentric layups // Journal of Reinforced Plastics and Composites. 2004. Vol. 23, no. 1. Pp. 5–16. DOI: 10.1177/0731684404028698
Об авторе
М. В. КаргаевРоссия
Каргаев Максим Владимирович, кандидат технических наук, доцент кафедры проектирования и сертификации авиационной техники ; руководитель группы
Москва; пос. Томилино
Рецензия
Для цитирования:
Каргаев М.В. Метод расчета устойчивости обшивок хвостовых отсеков лопастей несущего винта под действием ветра на стоянке вертолета. Научный вестник МГТУ ГА. 2025;28(5):63-75. https://doi.org/10.26467/2079-0619-2025-28-5-63-75
For citation:
Kargaev M.V. Method of stability computation of the main rotor blades tail section skins subject to wind at a helicopter parking lot. Civil Aviation High Technologies. 2025;28(5):63-75. (In Russ.) https://doi.org/10.26467/2079-0619-2025-28-5-63-75








































